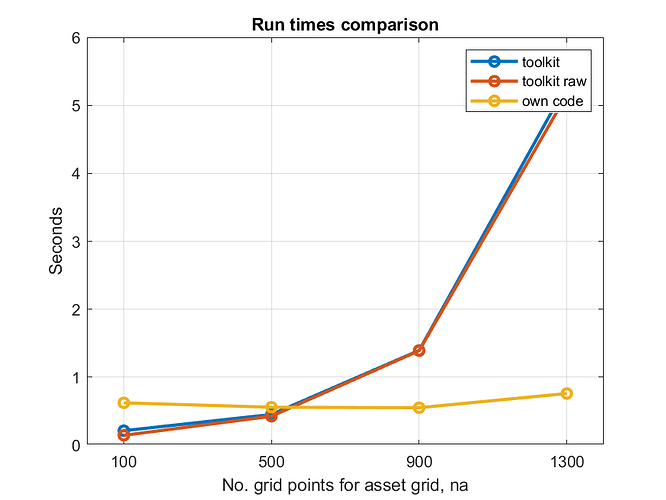
I did some run times comparison on the Aiyagari example with linear interpolation. I compared the toolkit with my own code (written as ValueFnIter_preGI_nod_raw but a few modifications) and I achieved a substantial perforamnce improvement over the toolkit method for grids with n_a>500.
Let me say upfront that the comparison is fair in the sense that I compare the kernel routine of the toolkit vs my own to avoid attributing overhead to the toolkit timings. (In the end this did not matter significantly since the toolkit overheads are very small).
The method I follow in my function VFI_interp_fast is very similar to the toolkit. In particular, I first solve the problem on a coarse grid for a', call it \mathcal(A) and find the policy function for next-period assets a'=g(a,z). Then I bracket the maximum in the interval (A(g(a,z)-1),A(g(a,z)+1) ) and I create a finer grid in this interval, with something like 15 points. I redo the grid search over a', restricting a' to lie on this new grid. But I avoid precomputing too much. Specifically I never precompute the return function on the finer grid.
I solve the Aiyagari VFI for different values of n_a (where n_a is the number of grid points in the coarse grid for A), ngridinterp=15 and n_z=11. n_a ranges from 100 to 1300; for each n_a, I solve the models 3 times and I average across the three repetitions. I compare three different methods:
- VFI Toolkit, this is the standard method called with
ValueFnIter_Case1 - Toolkit raw, which is a direct call to
ValueFnIter_preGI_nod_raw, to make the comparison as fair as possible. - My own code, in
VFI_interp_fast.
(I always check that VFI toolkit and toolkit raw give exactly the same results and that my own code gives very similar results)
The results are summarized in the plot below.
n_a from 100 to 1300, n_z = 11 and ngridinterp=15
The toolkit is faster only for small grids with n_a<500. For larger grid, the toolkit code becomes very inefficient due to the large memory requirements. Bear in mind that I keep n_z=11 which is realtively low (in a real model, you typically have more than one z shock…).
My codes for the comparison are on github: GitHub - aledinola/Aiyagari_Interpolation
It would be nice to see if these run times results hold true also on different computers/gpus. Also, I believe my code has room for further improvement, this is just a proof of concept.
This is the code for the comparison:
%% Run times comparison
n_a_vec = 100:400:1500;
n_a_vec_NN = length(n_a_vec);
N_rep = 3; % Number of repetitions to average out
timevfi_toolkit = zeros(n_a_vec_NN,N_rep);
timevfi_toolkit_raw = zeros(n_a_vec_NN,N_rep);
timevfi_fast = zeros(n_a_vec_NN,N_rep);
for i_a = 1:n_a_vec_NN
n_a = n_a_vec(i_a);
a_grid = 10*K_ss*(gpuArray(linspace(0,1,n_a)).^3)';
VKron = zeros(n_a,n_z,'gpuArray');
fprintf('Now doing n_a = %d \n',n_a)
for i_rep = 1:N_rep
disp(i_rep)
tic
[V1,Policy]=ValueFnIter_Case1(n_d,n_a,n_z,d_grid,a_grid,z_grid, pi_z, ReturnFn, Params, DiscountFactorParamNames, [], vfoptions);
timevfi_toolkit(i_a,i_rep) = toc;
tic
[V1_raw, Policy_raw]=ValueFnIter_preGI_nod_raw(VKron,n_a,n_z,a_grid,z_grid,pi_z,DiscountFactorParamsVec,ReturnFn,ReturnFnParams,vfoptions);
timevfi_toolkit_raw(i_a,i_rep) = toc;
if max(abs(V1-V1_raw),[],"all")>1e-8
error('Toolkit and Toolkit raw are not the same!')
end
% My own code
tic
[V2,pol_aprime2]=VFI_interp_fast(VKron,n_d,n_a,n_z,d_grid,a_grid,z_grid, pi_z, ReturnFn, Params, DiscountFactorParamNames,vfoptions);
timevfi_fast(i_a,i_rep)=toc;
end %end rep
end % end n_a