Fehr and Kindermann

[aledinola]

The textbook by Fehr and Kindermann on computational economics (see here) is a great resource for those interested in quant macro with Fortran.

In order to compare strengths and weaknesses of the VFI toolkit with the Fortran implementation of FK, I replicated the baseline life-cycle model of FK Chapter 10.1 with the toolkit. Interested users can find my codes here:

GitHub - aledinola/FehrKindermann_ch10_1

The model in a nutshell:
V(a,z,\theta,j) = \max_{a'} u(c)+\beta s_j E[V(a',z',\theta,j+1)|z]
subject to
c+a' = (1+r)a+w \kappa_j \exp(\theta+z)+pen_j, a'\geq 0,
where \kappa_j=0 for all j\geq J_R and pen_j=0 for all j<J_R. Here \theta is a permanent income type (college vs no college), \kappa_j is a deterministic age-profile and pen denotes pension benefits.

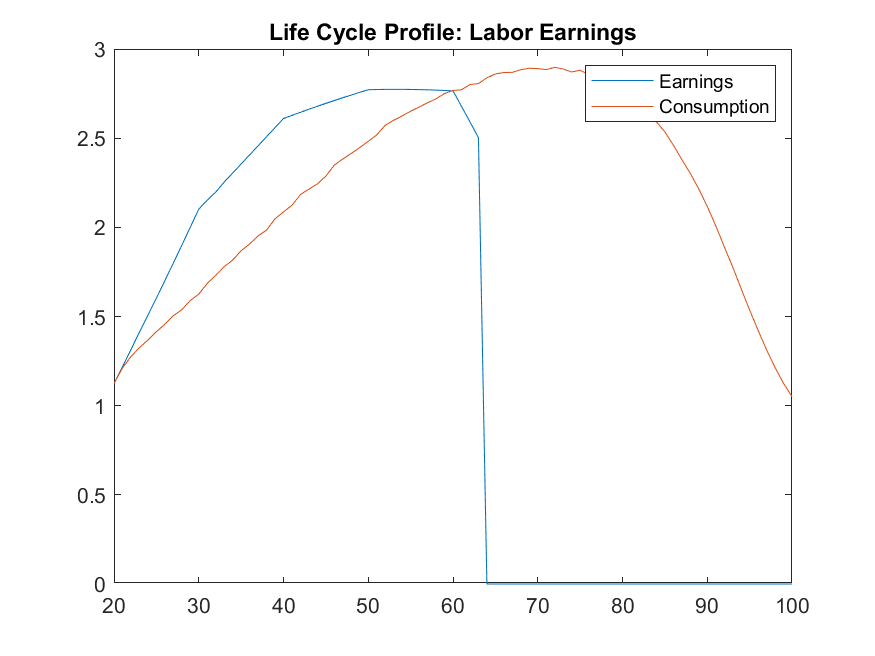
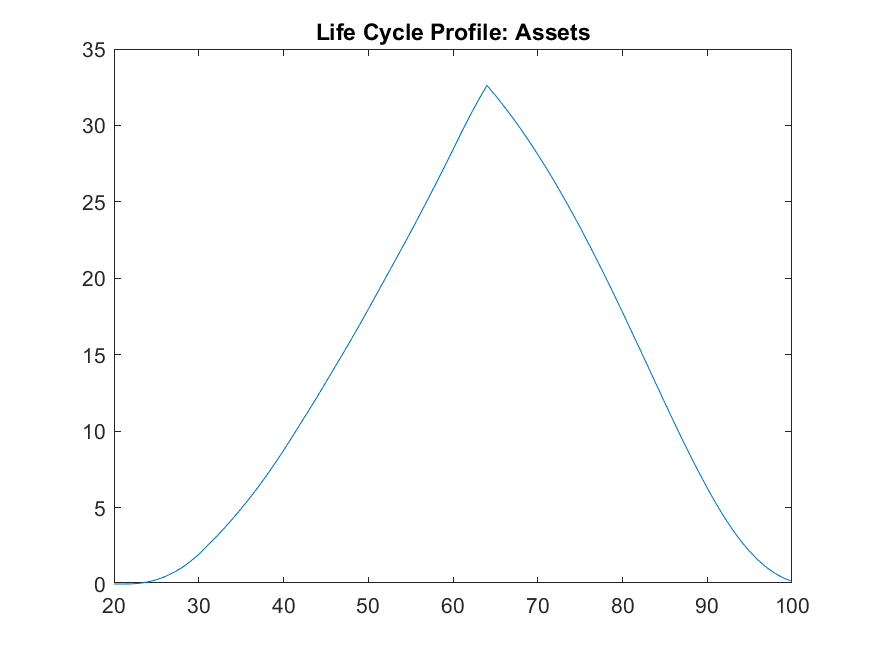
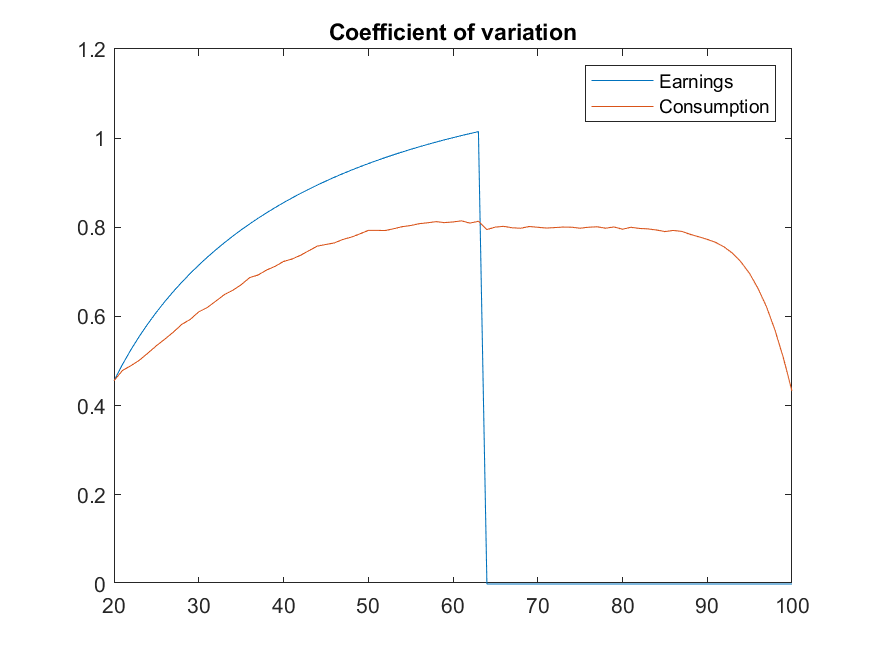
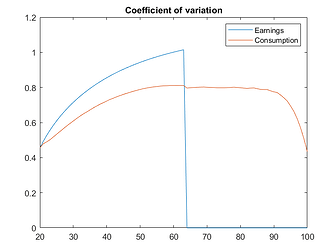
The results match almost exactly those of FK ch.10.1, which is a useful cross-check for the toolkit codes (and for their Fortran codes as well).

Performance

As, expected, the toolkit is slower than Fortran. The run times of the toolkit replication on my laptop (in seconds) are: (which admittedly does not have a very good GPU)

time_vfi = 2.546369 
time_distrib = 0.060441 
time_stats = 2.079527 (with simoptions.whichstats=[1,1,1,0,0,0,0];)

With divide and conquer on, the time for VFI improves a bit down to 1.9 seconds (but I have to manually set vfoptions.level1n = 7, with default value is slower.

In comparison the run time of the entire Fortran code (on the same laptop) is 0.3 seconds. A few things to observe:

• The Fortran code uses 200 grid points for assets but I use 1000 in order to get similar accuracy
• It took me half an hour to replicate the life-cycle model of FK, while writing the code in Fortran would take me one afternoon probably, with plenty of opportunities to make hard-to-catch mistakes.

Test case for finite-horizon model
If I have time I will test this code again with interpolation over a' to see how the trade-off between time and accuracy improves. Indeed, my idea was to prepare this nice life-cycle model of Fehr and Kindermann as a “test case” for toolkit improvements. We know exactly how the solution must look like, so hopefully this helps!

[robertdkirkby]

This is really cool!

Just to check I understand: for toolkit you use 1000 points with divide-and-conquer, for fortran it is 200 points with interpolation.

I will prioritise implementing the grid interpolation for this case (FHorz, no d, with z) so that it can be easily seen how the runtimes are impacted.

[aledinola]

Yes, and there is also a permanent type. More precisely, the model in Fehr and Kindermann has

• No d variable
• Asset holdings with n_a=200
• One Markov shock with n_z=7, AR(1) discretized with Rouwenhorst method
• Permanent income type \theta_i, two grid points
• J=80 for age

The solution method used by FK is based on Brent maximization with linear interpolation. Their Fortran codes are available here: ce-fortran/code-book/prog10/prog10_01/prog10_01.f90 at main · fabiankindermann/ce-fortran · GitHub

In my replication with the toolkit I just changed n_a to 1000 (with n_a=200 the plots look very zig-zag, which I interpret as very low accuracy). Divide and conquer improves the running time a bit but you have to set manually level1n

Update
It might be that in the Fortran code I shared, they use Euler equation method, not value function iteration. I am sure however that they have also the version with VFI somewhere. In any case, they always use linear interpolation. Anyways, this is a detail. I think makes it a good test.

[robertdkirkby]

Just pushed the code, you should be able to use vfoptions.gridinterplayer=1 for this now (although cannot yet do divide-and-conquer together with grid interpolation, I still need to implement that).

[aledinola]

I tried but I got this error:

Error using ValueFnIter_Case1_FHorz (line 68)
When using vfoptions.gridinterplayer=1 you must set vfoptoins.ngridinterp (number of points
to interpolate for aprime between each consecutive pair of points in a_grid)

[robertdkirkby]

As user you just set
vfoptions.gridinterplayer=1
which tells toolkit to use a ‘gridded interpolation layer’, and then use
vfoptions.ngridinterp=5
to say how many points to use for the interpolation.
And then you put the same into simoptions.

[aledinola]

Now I get this error:

Unrecognized function or variable ‘ValueFnIter_FHorz_GI_nod_raw’.

Error in ValueFnIter_Case1_FHorz (line 548)
[VKron,PolicyKron]=ValueFnIter_FHorz_GI_nod_raw(n_a, n_z, N_j, a_grid, z_gridvals_J, pi_z_J, ReturnFn, Parameters, DiscountFactorParamNames, ReturnFnParamNames, vfoptions);
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_Case1_FHorz_PType (line 145)
[V_ii, Policy_ii]=ValueFnIter_Case1_FHorz(n_d_temp,n_a_temp,n_z_temp,N_j_temp,d_grid_temp, a_grid_temp, z_grid_temp, pi_z_temp, ReturnFn_temp, Parameters_temp, DiscountFactorParamNames_temp, , vfoptions_temp);
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in main (line 119)
[V, Policy]=ValueFnIter_Case1_FHorz_PType(n_d,n_a,n_z,N_j,N_i, d_grid, a_grid, z_grid, pi_z, ReturnFn, Params, DiscountFactorParamNames, vfoptions);
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

[robertdkirkby]

sorry, pushed now (missed it before)

[aledinola]

Now VFI runs but I get this mistake. Note: this mistake happens also if vfoptions.gridinterplayer = 0; On the plus side, interpolation with n_a=200 and n_interp=15 seems fast

Output argument "StationaryDist" (and possibly others) not assigned a value in the execution
with "StationaryDist_FHorz_Case1" function.

Error in StationaryDist_Case1_FHorz_PType (line 187)
        StationaryDist_ii=StationaryDist_FHorz_Case1(jequaloneDist_temp,AgeWeightParamNames_temp,Policy_temp,n_d_temp,n_a_temp,n_z_temp,N_j_temp,pi_z_temp,Parameters_temp,simoptions_temp);
                          ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in main (line 155)
StationaryDist=StationaryDist_Case1_FHorz_PType(jequaloneDist,AgeWeightsParamNames,PTypeDistParamNames,Policy,n_d,n_a,n_z,N_j,N_i,pi_z,Params,simoptions);
               ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

[robertdkirkby]

Do you have:
simoptions.gridinterplayer=vfoptions.gridinterplayer
simoptions.ngridinterp=vfoptions.ngridinterp

[aledinola]

Fixed that, thanks!

Version 1. Run times with n_a=350 and ngridinterp=15

time_vfi = 1.073664 
time_distrib = 0.045535 
time_stats = 1.569840 

Version 2. Run times with n_a=1000 and NO interpolation:

time_vfi = 2.314069 
time_distrib = 0.058532 
time_stats = 1.901379 

In terms of accuracy, I think the two versions (1) and (2) are comparable. Looking e.g. at the coefficient of variation for consumption over the lifecycle, we have

No interpolation with n_a=1000

Interpolation with n_a=350

The results for interpolation are quite good in terms of making the code faster! Please note that for many model moments you could further reduce the number of grid points with interpolation. I tried a version with only n_a=200 and was quite good for averages. As a caveat, I talk about accuracy very sloppily, one should do Euler equation errors and more formal tests.

Comparison with Fortran

Very rough: the entire Fortran code takes 0.3 seconds. The toolkit with interpolation, vfi plus distribution take 1.1-1.15 seconds. Not bad! (I do not include the timings for the statistics because I think there is still a lot of room for improvement. In Fortran they take a split of a second also because the Fortran code computes only the statistics that are needed, while the toolkit computes more stuff, even when using the option whichstats).

[aledinola]

I have an update: if I run the same version with linear interpolation, but setting the permanent income type \theta_i as a second Markov shock, the run times improve even further (as expected):

Version 1 . Run times with n_a=350 and ngridinterp=15 and PT includes as z2

time_vfi = 0.660919 
time_distrib = 0.049698 
time_stats = 0.407692

[robertdkirkby]

This model should now work with both vfoptions.divideandconquer=1 and vfoptions.gridinterplayer=1 together. I suspect that in this case the model is small enough that it will actually be slower to divide-and-conquer, but still cool that both together works so smoothly.

[robertdkirkby]

Just to comment that Fehr & Kinderman fortran codes for 10.1 calculate the agent distribution by iteration, and then get the stats directly from this agent distribution. So they are taking essentially the same approach as toolkit in this respect. [VFI Toolkit implements the details slightly differently, but my point is that neither simulates the agent distribution.]

And their main fortan code is 440ish lines, vs 210ish lines for Alessandro’s matlab (subcodes are then another 150 and 40 lines, respectively).

[aledinola]

Yes, Fehr and Kindermann compute the endogenous distribution in their subroutine get_distribution using linear interpolation. Interestingly, they don’t use the Tan improvement
They also don’t take advantage of the sparsity of the transition operator (this is one of the advantages of using Matlab)

Once they have the distribution and the policy functions, they compute several moments conditional on age in the subroutine aggregation. Their code is well written, but is very “model-specific”.

[aledinola]

I tried it and got the error shown below when calling the distribution. Besides the error, performance is worse (VFI goes from 0.6 seconds to 1.1 seconds). I have updated my repo on github: if you want to reproduce the error, please run main_noPT.

Here are my options:

% Options
vfoptions.verbose=1; % Just so we can see feedback on progress
vfoptions.divideandconquer = 1;
vfoptions.gridinterplayer  = 1;
vfoptions.ngridinterp      = 15;
simoptions.gridinterplayer  = vfoptions.gridinterplayer;
simoptions.ngridinterp      = vfoptions.ngridinterp;

Error message

Index exceeds matrix dimension.

Error in StationaryDist_FHorz_GI_raw (line 27)
    aprimeProbs=shiftdim((simoptions.ngridinterp+1-Policy(l_d+2,:,:,1,:)+1)/(simoptions.ngridinterp+1),1); % probability of lower grid point
                                                   ^^^^^^^^^^^^^^^^^^^^^
Error in StationaryDist_FHorz_Case1 (line 232)
                StationaryDist=StationaryDist_FHorz_GI_raw(jequaloneDist,AgeWeightParamNames,Policy,n_d,n_a,n_z,N_j,pi_z_J,Parameters,simoptions);
                               ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in main_noPT (line 151)
StationaryDist=StationaryDist_FHorz_Case1(jequaloneDist,AgeWeightsParamNames,Policy,n_d,n_a,n_z,N_j,pi_z,Params,simoptions);

[robertdkirkby]

Fixed the error.

Yeah, fits with my impressions so far, which is that GridInterpLayer is good for everything, and divide-and-conquer is good for everything except small problems where is is counterproductive. [I suspect what constitutes ‘small’ will be heavily dependent on the GPU]

[aledinola]

Thanks! Distribution code works with the combo divide and conquer + interpolation.