Grid interpolation in Infinite horizon models

1

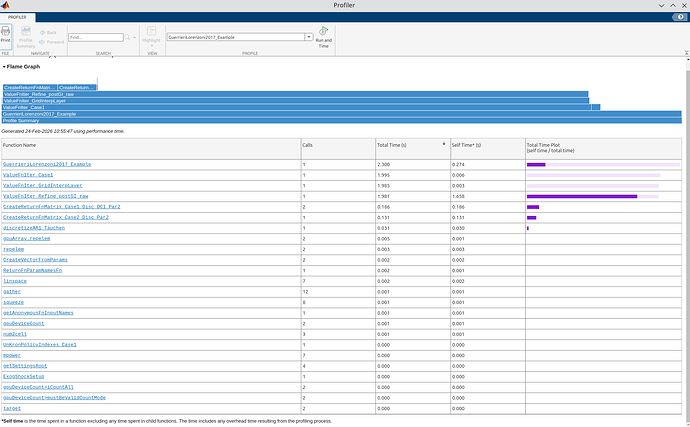
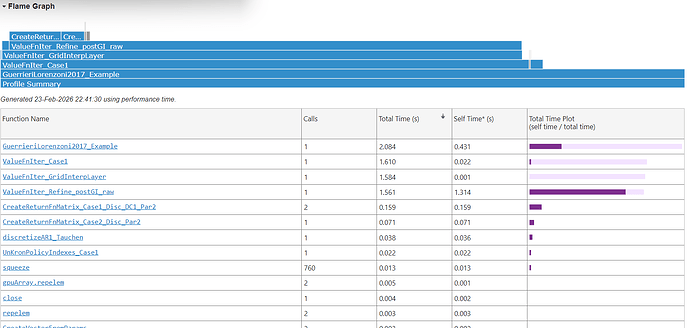
I think I found a bug in ValueFnIter_Refine_postGI_raw. I wanted to disable the Howard improvement step to do some checks, so I set vfoptions.maxhowards= 0, as suggested by @robertdkirkby, but I got this error message:

Index exceeds matrix dimension.

Error in ValueFnIter_Refine_postGI_raw (line 276)
Policy(1,:,:)=reshape(dstar(temppolicyindex),[N_a,N_z]);
                      ^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_GridInterpLayer (line 149)
                    [V,Policy]=ValueFnIter_Refine_postGI_raw(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
                               ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_Case1 (line 465)
    [V,Policy]=ValueFnIter_GridInterpLayer(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
               ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in main (line 193)
[~, Policy] = ValueFnIter_Case1( ...
              ^^^^^^^^^^^^^^^^^^^^^^

Of course in practice one would never want to disable Howard, but I thought it’s worth to point this out. This brings me to another issue that I have encountered. I wanted to stress-test the routine that I have written for grid interpolation with d variable and Howard sparse and compare it to the default routine in the toolkit. The two routines are

  • ValueFnIter_Refine_postGI_raw default, which works well
  • ValueFnIter_postGI_sparse_raw new routine

In the Pijoan-Mas model, I have found a specific parameterization where unfortunately ValueFnIter_postGI_sparse_raw fails to converge. Here is the code: PijoanMasTaxes/main.m at main · aledinola/PijoanMasTaxes · GitHub

I set the usual options:

vfoptions.howardsgreedy = 0;
vfoptions.howardssparse = 0;
vfoptions.gridinterplayer = 1;
vfoptions.ngridinterp     = 15;

This calls the default for interpolation, which is ValueFnIter_Refine_postGI_raw and it runs well. When I set vfoptions.howardssparse = 1; the code calls instead ValueFnIter_postGI_sparse_raw and unfortunately it fails to converge: the distance (variable currdist) goes down initially but then it oscillates between 0.0002 and 0.0003

@robertdkirkby I was very happy when you accepted this contribution in the toolkit but it seems that my function, although faster, is less stable than yours :face_with_open_eyes_and_hand_over_mouth:. Do you happen to see some easy-to-spot inaccuracy or lack of robusteness in the code of ValueFnIter_postGI_sparse_raw? VFIToolkit-matlab/ValueFnIter/InfHorz/GridInterpLayer/ValueFnIter_postGI_sparse_raw.m at master · vfitoolkit/VFIToolkit-matlab · GitHub

If I increase the number of grid points from n_a=600 to n_a=700, my function converges. However I’m struggling to understand where the problem might be compared to the default function that always converges no matter what.

1 Like
2

I found another issue with the toolkit function ValueFnIter_Refine_postGI_raw.m (this is one of the default functions, I think). I noticed that we are still using interpMatrix in a couple of places. For me is fine, but based on our previous discussion we had decided not to use it for the time being, due to some potential inconsistencies with -Inf that @MichaelTiemann found out?

1 Like
3

It happened to me that I go out of memory when I reach that line in the code (with the multiplication of interpmatrix with EV). So I went back to the solution without interpolation but it is a pity since it is less accurate.

2 Likes
4

Fixing/improving ValueFnIter_Refine_postGI_raw.m is a priority for me, in particular finding a good way to implement the interpolation step. But I am away on holidays for the next two weeks, so it is a priority that I won’t get to until I return.

@javier_fernan good to know that this can be a memory bottleneck, I was not aware.

1 Like