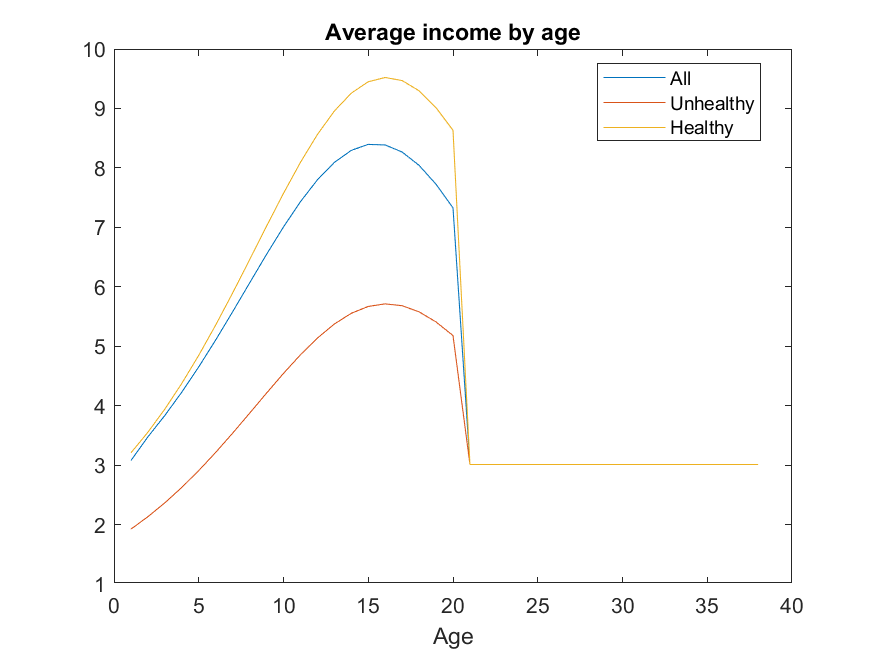I have created a simple example on Github, available here: https://github.com/aledinola/Endogenous_survival/tree/main
to show how to code a lifecycle model with endogenous survival rate. The model has the following state variables:
- Asset holdings, a, which is an endogenous state
- Health state h=0,1, which is an age-dependent Markov shock. h=0 for unhealthy and h=1 for healthy
- Labor productivity y, which is another Markov shock
- Age j
The labor productivity shock y is discretized using Tauchen. The transition probabilities for h depend on age: let p_{00}(j) denote the probability that h^{\prime}=0 given h=0 and age j, and let p_{11}(j) denote the probability that h^{\prime}=1 given h=1 and age j. It makes sense to assume that p_{00}(j), the probability of remaining sick, is increasing with age, while p_{11}(j) is decreasing with age.
To allow the survival probability to depend on health, we add a third state to h, and call it h=2 if the agent is dead. Then we can define the probability of, say, going from h=0 to h=1 as s(h=0,j)(1-p_{00}(j)). This is the probability of surviving into the next period, times one minus the probability of remaining sick. In matrix form,
\begin{bmatrix} s(h=0,j)p_{00}(j) & s(h=0,j)(1-p_{00}(j)) & 1-s(h=0,j) \\ s(h=1,j)(1-p_{11}(j)) & s(h=1,j)p_{11}(j) & 1-s(h=1,j) \\ 0 & 0 & 1 \end{bmatrix}
Observe that the survival probability s(h_j,j) depends not only on age j, as standard, but also on a state variable, namely h. Observe furthermore that the last row of the matrix above gives the probability of transitioning out of h=2 (dead is an absorbing state)
How to code this in the toolkit?
You define the transition probability for health h as follows:
pi_h = zeros(n_z(1),n_z(1),N_j);
for jj=1:N_j
% h=0 h=1 h=2
temp = [sj_h0(jj)*p_00(jj), sj_h0(jj)*(1-p_00(jj)), 1-sj_h0(jj);
sj_h1(jj)*(1-p_11(jj)), sj_h1(jj)*p_11(jj), 1-sj_h1(jj);
0, 0, 1 ];
pi_h(:,:,jj) = temp;
end
You define only the discount factor beta as a discount factor parameter. Normally we would also add sj, but here we don’t do that since sj is incorporated into the transition of the health shock h.
DiscountFactorParamNames={'beta'};
The return function is coded as follows:
function F = Mod_ReturnFn(aprime,a,h,y,agej,Jr,kappa_j,r,wp,y_pen,sigma)
%INPUT ARGUMENTS
% aprime: Next-period assets, endogenous state choice
% a: Current assets, endogenous state
% h: Health status, exogenous state (Markov)
% y: Labor productivity shock, exogenous state (Markov)
% agej: Age
F=-Inf;
if h==2
% Dead
F = 0;
return
end
wage_penalty = -inf; %hopefully gives error if not overwritten
if h==0
% Unhealthy
wage_penalty = wp;
elseif h==1
% Healthy
wage_penalty = 0;
end
if agej<Jr
% Working age
cons = (1+r)*a+exp(kappa_j+y)*(1-wage_penalty)-aprime;
else
% Retired
cons = (1+r)*a+y_pen-aprime;
end
if cons>0
F = cons^(1-sigma)/(1-sigma);
end
end %end function
Note that if h=2 the agent is dead and we assign a return equal to zero (here, the value of death is implicitly zero).
Last but not least, when we compute the model statistics (e.g. mean assets or mean earnings) we have to condition on the agents being alive, i.e. on h=0 or h=1. We do this as follows:
condres.alive = @(aprime,a,h,y) (h==0 || h==1);
condres.h0 = @(aprime,a,h,y) (h==0); % unhealthy
condres.h1 = @(aprime,a,h,y) (h==1); % healthy
If we want average assets by age for everyone, we select AgeStats.alive.assets.Mean. But of course we are also interested on assets conditional on being unhealthy or healthy, and this is why we have two additional restrictions.
Possible bug
@robertdkirkby I think I found this issue also in a previous code some time ago. When I plot the earnings, everthing looks fine
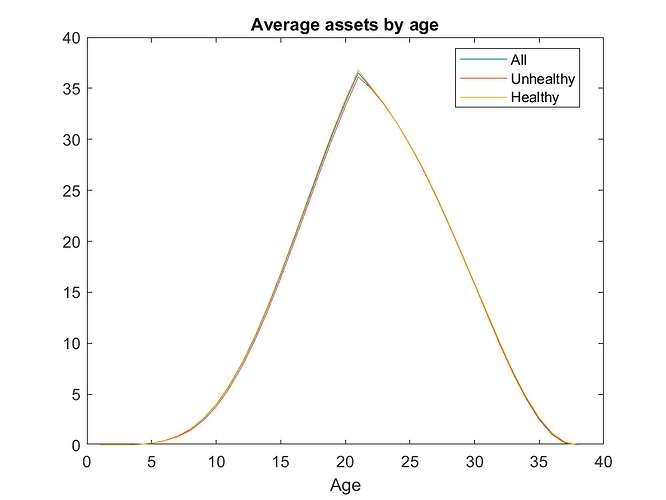
but for assets I get something strange
This can’t be right (it is ok, please see post below) because I set a substantial wage penalty for unhealthy (they lose 40% of their income), which shows up in earnings, but not in assets. I think there was the same problem in another example of mine, if I find the discourse post I will add the link here.
UPDATE
Here is the post about the old bug (December 2024). In the old post, I was using Ptypes, but in this example, I do NOT have PTypes.