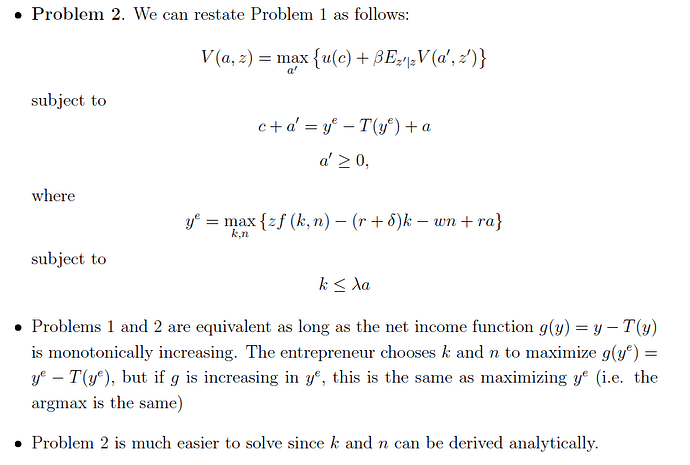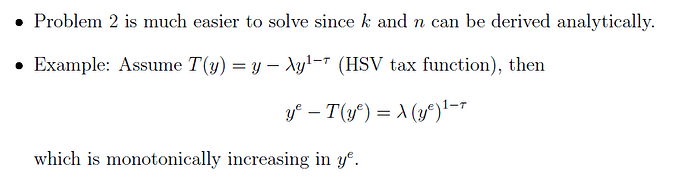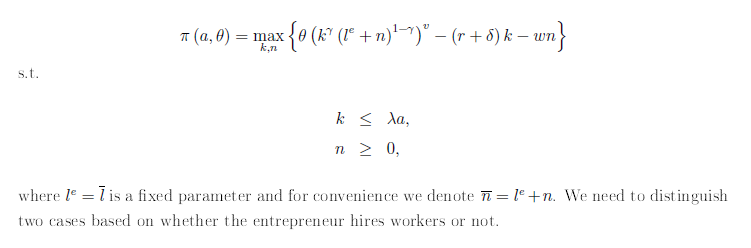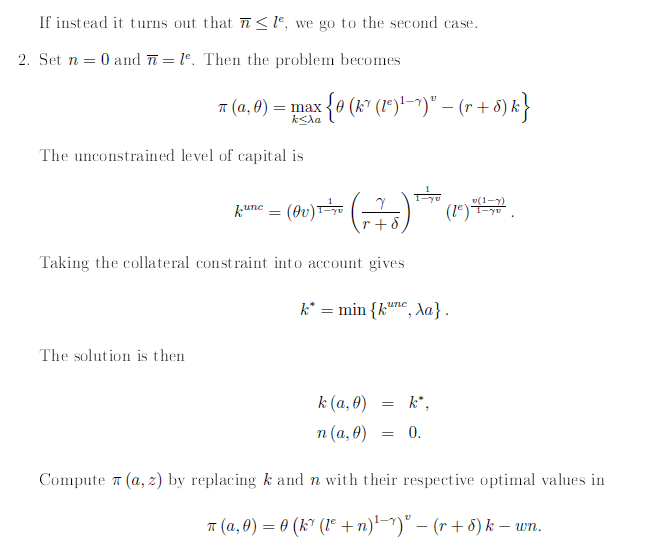I’d like to share on the forum some simple thoughts on solving models with entrepreneurs. Examples of heterogeneous agents models with entrepreneurs are, among many others,
- Bettina Brueggemann, 2017.
“Higher Taxes at the Top: The Role of Entrepreneurs,”
Department of Economics Working Papers 2017-16, McMaster University.
https://ideas.repec.org/p/mcm/deptwp/2017-16.html, later published on AEJMacro 2021. - Sagiri Kitao, 2008.
“Entrepreneurship, taxation and capital investment,” Review of Economic Dynamics, Elsevier for the Society for Economic Dynamics, vol. 11(1), pages 44-69, January.
https://ideas.repec.org/a/red/issued/06-33.html
When solving these models with the VFI toolkit, one runs easily into memory problems since one has to define at least two decision variables d in addition to the standard endogenous and exogenous states. Typically, we have capital and labor demanded by entrepreneurs (Kitao 2008), or labor supply, capital and labor (Bruggeman 2021).
If the model is infinite horizon, one can solve for the steady state using the “refinement” option which essentially precomputes the optimal d before the VFI loop starts. This trick, however, is not available for transitional dynamics or more generally for finite horizon/OLG models.
However, in almost all cases that I’ve seen, one can easily derive the optimal values for k and n analytically (ok, not labor supply…), there is no need to use a grid. This is true as long as the entrepreneur’s after tax income is monotonically increasing in taxable income, which is almost always satisfied. I attach below a short note that I’ve written.
Let’s start with the original formulation of the entrepreneurs’ problem (essentially copied and pasted from Bruggeman 2021):
Toolkit: a is endogenous state, z is Markov exogenous state and d=(k,n) are two static decisions.
It turns out that the problem can be rewritten equivalently as:
The attached text explains why. As an example, one can assume that T() is a progressive tax function as in Heathcote, Storesletten and Violante (XXX), but T does not have to be differentiable of course.
Why is this progress? Because we can derive k and n analyticaly, so they don’t have to be included as d variables. Let’s assume a functional form for the production function f(k,n) as below (basically, a decreasing returns to scale production function as in Lucas (1978))
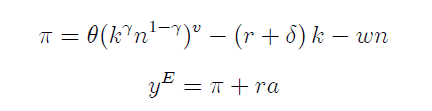
then we can take FOCs and obtain a closed-form solution:
Note: in my note above, assume that theta=z (entrepreneurial ability or productivity)