Looking at infinite horizon models with d variable (e.g. Pijoan-Mas RED 2006, Boar and Midrigan (JME 2022) or Bruggeman AEJ:Macro).
The toolkit now can use a finer grid for a’ with interpolation, so a’ is not restricted anymore to lie on a_grid.
Is it possible to solve for d(a',a,z) in multiple layers? So the first time the optimal d is chosen from d grid. Once we know d*, we create another grid between d*-1 and d*+1 and find optimal d on this second grid. Here we don’t even need to interpolate, since the return function is known.
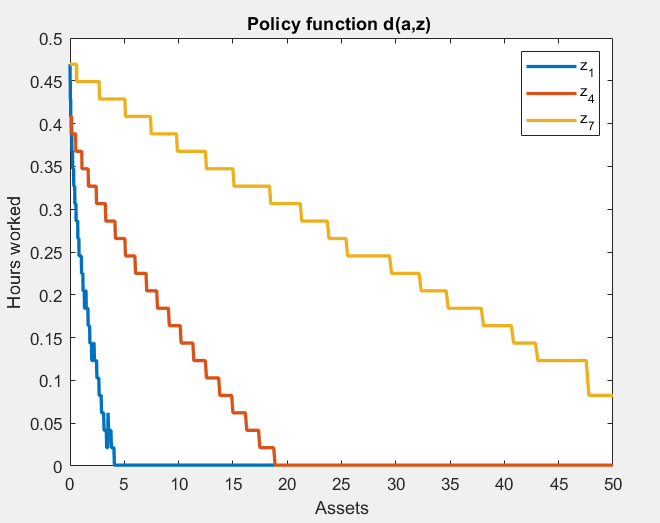
I am asking about this since I noticed that in these models the policy for d has a weird zig-zag pattern that is an artefact of the grid, so the results may not be very accurate.
You mean solve d onto a ‘fine grid’ in a manner like how a’ is solved on a ‘fine grid’ with grid interpolation layer?
I have been thinking about some kind of approach like this. Kind of need to know two things, the first is ‘monotonicity’ of d (or at least something that guarantees the optimal on the fine grid is going to be next to the optimal on the rough grid), the second is how to handle multidimensional d (easy enough, just only do this for the first dimension of d, and user just needs to set up appropriately).
Currently I have not implemented something like this, but I am actively thinking about how to either do a ‘divide-and-conquer’ or a ‘grid interpolation layer’ approach to decision variables in infinite horizon together with ‘refine’. This kind of things will work nicely with the ‘postGI’ approach for aprime.
PS. Based on my experience with replications, if you put 101 points on labor supply this is accurate enough (201 points gives little to no change in solution).
1 Like
Btw, there are some improvements around postGI sitting on my harddrive. I will push them in January. I am off on holiday on Friday so don’t want to push now in case they break things just as I disappear for the rest of the year. They mean I can easy solve Bruggemann (2022) even with the 300 points on labour, just on my desktop.
1 Like
Nice! Could you please send me by email the files for Bruggeman? I am working on a similar model and they can be helpful (plus I can proofread the replication)
Will email later this week, just want to do a bit more cleanup first.
1 Like
I was doing some experiments on my repo with Pijoan-Mas to test accuracy of toolkit solving infinite horizon models with a d variable (typically, labor supply). Here are the results.
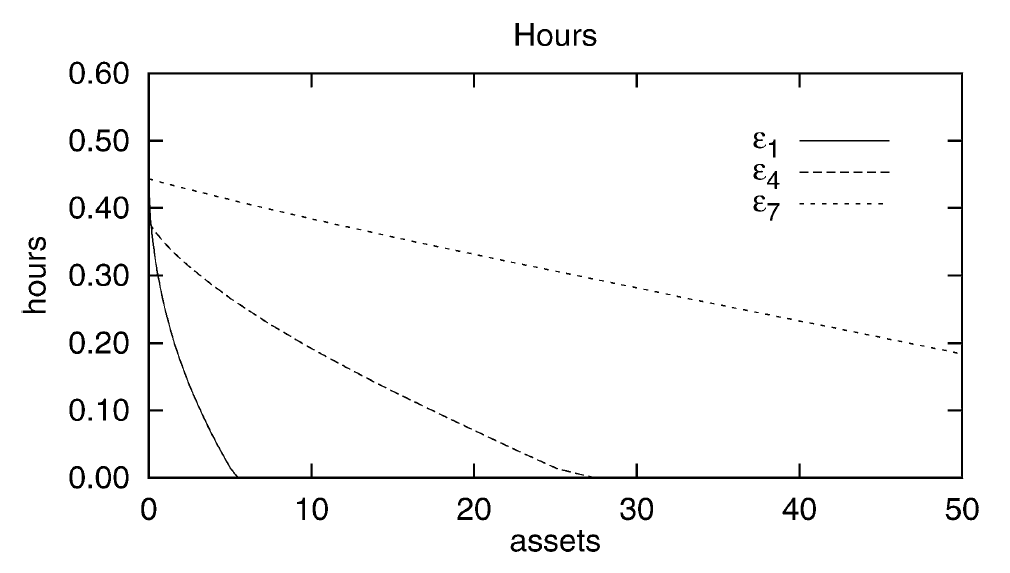
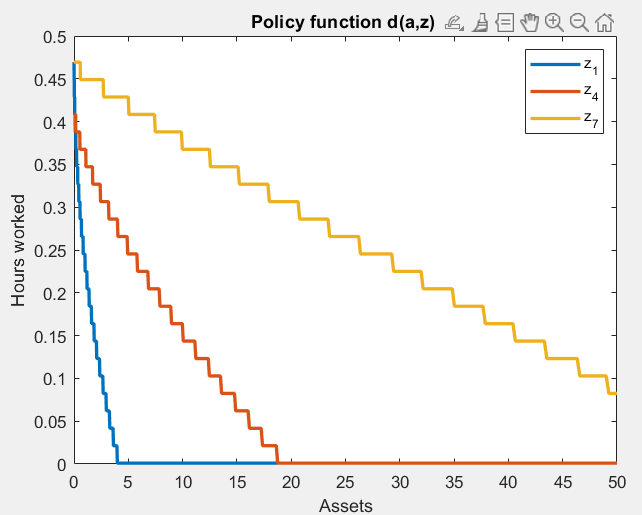
From Pijoan-Mas paper, I want to replicate the plot of the olicy function for hours worked
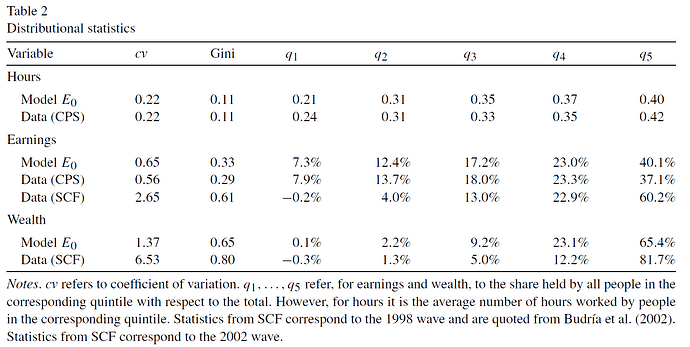
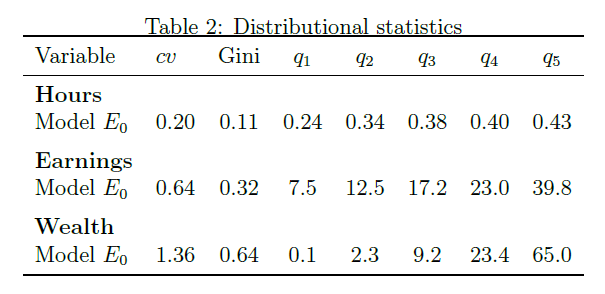
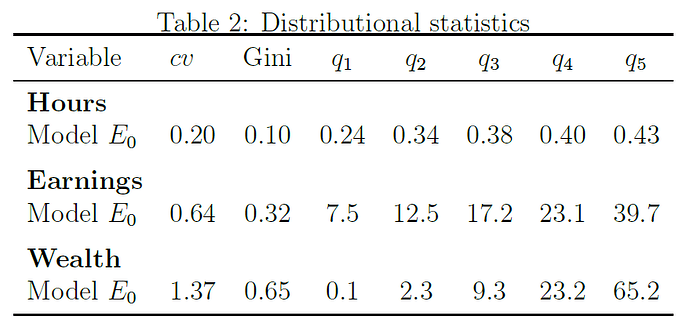
and this table with model moments on the distribution of hours worked, income and wealth in the benchmark model
Let’s try first with pure discretization (fast and robust but not very accurate) and then with interpolation (slower but more accurate).
Pure discretization (i.e. a' restricted on the same grid of a)
Policy function for hours worked:
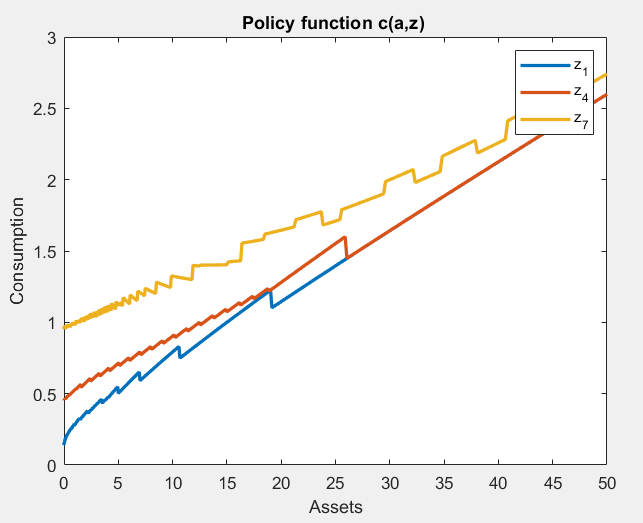
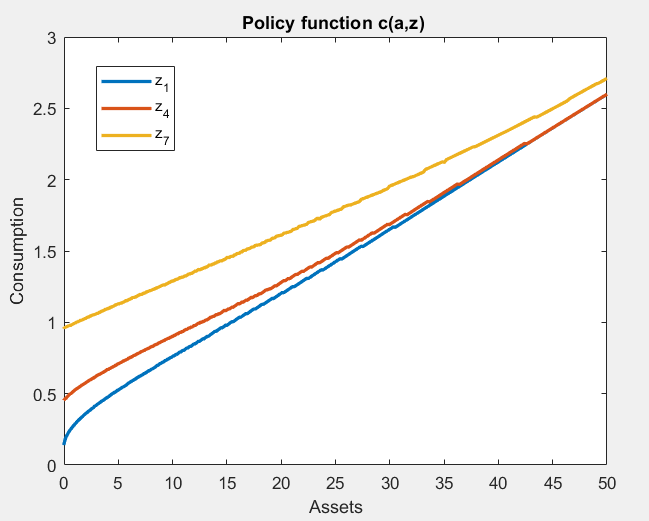
Let’s see also the policy for consumption:
And then the table:
Interpolation (i.e. a' NOT restricted on the same grid of a)
Policy for hours worked:
Policy for consumption:
Table:
Conclusion
What seems quite off with discretization is the policy for consumption. The inequality statistics are largely unaffected, but there is nothing regarding consumption inequality. It could be that discretization biases moments related to consumption, at least by looking at how inaccurate the policy function is.