Replication of Huggett (JME 1997)

17

Very interesting! I have not managed yet to run the transition using the vfi toolkit, but I have coded myself the Huggett 1997 model. The files are available in my repo here: GitHub - aledinola/Huggett_1997, see folder cpu.

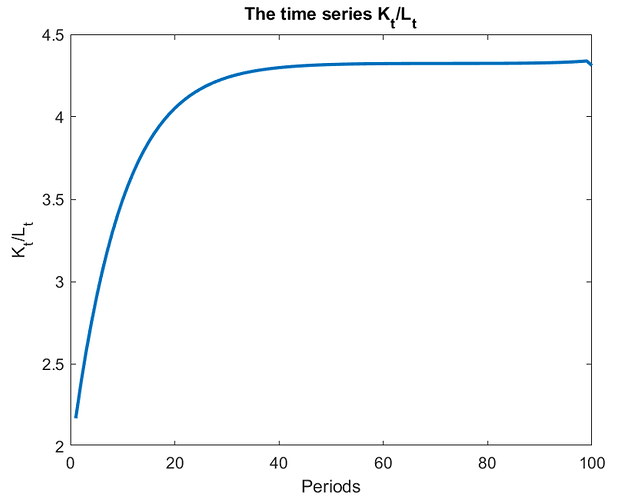
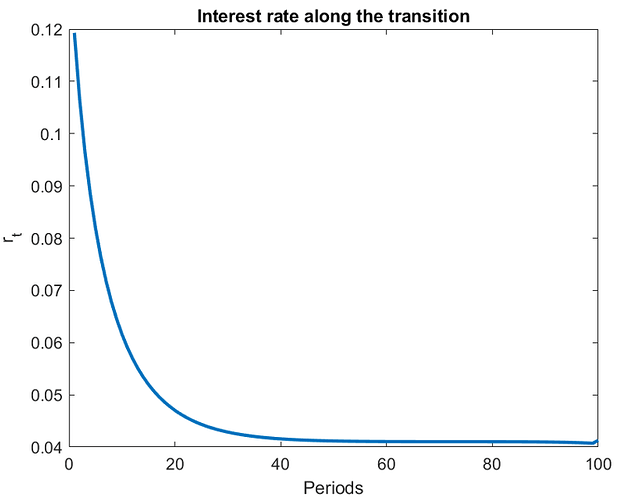
I set T = 100 and the transition converges, getting similar results to what you have shown. I have a number of observations that I summarize below:

  • I set a high number of grid points for assets, na=2000, to make sure the computation is accurate enough. The model is simple so we can afford many grid points.
  • I compare the stationary equilibrium in my code and in the toolkit and there are small differences, using exactly the same parameters for tolerance, max number of iterations etc.
    Toolkit results:
RESULTS FINAL STEADY STATE, VFI TOOLKIT
Algorithm: pure discretization
No. grid points assets: 2000 
CapitalMarket residual: -0.004739 
Goods market residual:  -0.000195 
Aggregate capital:      4.311640 
Capital-to-labor ratio:  4.311640 
Capital-to-output ratio: 2.547835 
Consumption:             1.261308 
Interest rate:           0.041296 
Wage:                    1.083057 
Run time General Equil: 8.772723

My code results:

FINAL STEADY-STATE, OWN CPU CODE: 
Algorithm: pure discretization
No. grid points assets: 2000 
CapitalMarket residual: 0.001356 
Goods market residual:  0.000052 
Capital stock:           4.311645 
Capital-to-labor ratio:  4.311645 
Capital-to-output ratio: 2.547836 
Consumption:             1.261061 
Interest rate:           0.041296 
Wage:                    1.083057 
Run time General Equil: 6.970329
  • As I said, I am not able to compute the transition with the toolkit, but I computed it with my code and it converges with tolerance = 10^(-3) and T=100 and dampening parameter equal to 0.9
  • The transition seems pretty robust but completely different from what Huggett (1997) reports.
  • As @yechen observed, I also noticed that towards the end, K(t) seems to drift down. Does this mean that the transition is not accurate? I don’t know. I had found a similar problem in this older post.

image
image758×612 27.6 KB

image
image759×603 33.8 KB

In the first plot above I show K(t)/L(t) but this is the same as K(t) since average labor is always equal to 1 in this particular model.

Update
Huggett (1997) writes that he used T=1000 while I used T=100. I will recompute the transition with T=1000, but I am sceptical that the results will change substantially. I assume the original code is not available since this is an old paper…

1 Like