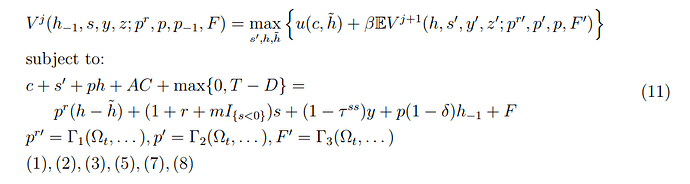Was writing the following as an email, figured I would clean it up for general interest
A Rough Guide to Getting Inequality in OLGs
We are often interested in getting realistic levels of inequality in life-cycle and OLG models. This is a brief description of how this is typically done and covers various aspects of inequality: earnings, consumption, wealth, and hours worked. I focus on the most basic/standard approaches.
Earnings Inequality
In an exogenous labor supply model, earnings inequality is directly generated by our process on earnings. In an endogenous labor supply model earnings inequality is a combination of the process on earnings with decisions on how much to work. Here I will describe the case with exogenous labor supply, but most of the literature with endogenous labor supply simply does the same things, except as a process on earnings-per-unit-of-time-worked, rather than as a process on earnings.
The ‘standard’ approach (as of early 2020s) is to model earnings as
earnings=exp(\alpha_i+\kappa_j+z+e)
Where \alpha_i is a fixed-effect, \kappa_j is a deterministic age-profile (often fitted as a quadratic or cubic function), z is an AR(1) process, and e is an i.i.d. process. [The exponential is there as then we can estimate this from data on log-earnings, and because it eases the interpretation of \alpha_i, \kappa_j, z and e as they are ‘percentage deviations’.]
This process is capable of generating realistic earnings inequality (e.g., all the deciles). But we can do substantially better with a few small changes. The first is to make the parameters of z and e depend on age. The second is to change the innovations to z and e, which are typically normal/gaussian distributions, and instead to use gaussian-mixture innovations.[VFI Toolkit contains routines to discretize all of these, see Appendix on exogenous shock processes in the Intro to Life-Cycle Models.]
Two more things we might add to earnings to make them more realistic. The first is a ‘heterogeneous income profile’ (HIP), essentially instead of the fixed effect, \alpha_i, being a constant, we can also have a slope \alpha^{HIP}_i * j which generates an ‘income profile’ [Think of it as a reduced-form approximation of modelling human capital that is accumulated with age/work and which impacts earnings.] The second is that we estimate different earnings profiles for different educational groups. [GKOS2023 and Blundell, Graber & Mogstad (2015) advocate these two, respectively.]
There is one last thing worth mentioning for earnings inequality. Adding a ‘non-employment’ shock can help hit earnings[Later I emphasize non-employment shocks as a way to hit hours-worked inequality, but they also help for earnings.] You can either use a ‘partial non-employment’ shock (if you are hit with shock, earnings are 0.7 of what they would otherwise be), or full non-employment shocks (if you are hit with shock, earnings are zero).[Kaplan (2012) does partial, GKOS2022 does full.]
People used to use unit-root/permanent shocks. An estimation like that of GKOS2022 would estimate an age-conditional autocorrelation of one if this was the ‘correct’ process. They do not. This kind of evidence strongly suggests permanent shocks are not very empirically realistic.
Getting earnings inequality ‘right’ obviously has important impacts on getting consumption and wealth inequality.
Consumption Inequality
Consumption inequality in the data increases with age. As long as your earnings process gives a substantial role to permanent/persistent shocks, and/or to heterogeneous income profiles (and you have a tight borrowing constraint for the young), your model is going to get this just fine. Obviously getting the details is trickier, but the broad-brush is easy enough. See, e.g., Storeslettern, Telmer & Yaron (2004).
Wealth Inequality
Wealth inequality is substantially higher than earnings inequality (in the data). There are two sides to getting it empirically roughly right. First is to get that a decent chunk of the population has essentially zero fraction of total wealth (but not quite zero wealth), the second is to get that the top 10/5/1% hold an obscenely large amount. Getting that a chunk of the population holds near zero can be done in two ways: have a flat-earnings profile together with a pension that is roughly the same amount as their earnings (this kills off the life-cycle consumption-smoothing motive for saving), or you can have them be relatively impatient (either have different agents with different discount factor, beta, those with lower beta will solve little to nothing given equilibrium interest rates; or make them suffer impatience (quasi-hyperbolic discounting) or temptation (Gul-Pesendorfer preferences). [VFI Toolkit can handle any/all of these using permanent types.]
There are roughly three ways to get the wealth inequality at the top of the wealth distribution: (i) bequests, (ii) preference heterogeneity (typically different discount factors), (iii) heterogeneous rates of return. Note that without bequests, the effect of all the others is muted. Often the heterogeneous rates of return are more explicitly modelled as entrepreneurship. For the top quintile of wealth, and for the savings of the elderly, the risk of medical expenses in old age can be modelled explicitly. When using bequests the intergenerational persistence of earnings ability is also important. See De Nardi & Fella (2017) for more. The heterogeneous rates of returns is easily implemented in a standard life-cycle model where there is a rate-of-return r to assets, simply making r stochastic (more persistent markov processes will generate more wealth inequality).
Hours Worked Inequality
If you just add endogenous labor as a (continuous) decision you won’t capture hours worked inequality. There are two levels at which you can get the hours worked inequality. The first is to use non-employment shocks to simply force people to be occasionally unable to work (and allow them to depend on age), you can find this in Kaplan (2012). The second endogenizes more and uses labor-search (you can decide to try find a job, but only end up with a job with some probability; model employment-status as a ‘semi-exogenous state;) together with earnings being a convex function of hours worked and a fixed-cost of working (Erosa, Fuster & Kambourov, 2016).
Initial Inequality
Your model is likely to start in period 1 with everyone already being, e.g., 23 years old. Inequality already exists at this age, and will simply have to be put into the model in the form of the initial age j=1 distribution.[Obviously the more state variables and permanent types in the model, the easier it is to have a lot of heterogeneity/inequality in the age j=1 distribution.] To give a simple example, imagine the model has one endogenous state for assets, and one markov exogenous state for earnings. We could estimate a joint log-normal iid distribution for assets and earnings from the data on 23 year olds, and then discretize this as our age j=1 distribution. [Log-normal as the empirical distributions have a skew towards high earnings/assets, and the log-normal is a simple way to capture this which normal would not be able to do. Even better might be something like gaussian-mixture.]
A few final points
Another thing we might want to get in terms of inequality is family/gender, Borella, De Nardi & Yang (2018) is a nice example. Human capital is going to be important in terms of getting earnings inequality and how it reacts to any changes in the economy. We might also be interested in making education endogenous.