Test infinite horizon with grid interpolation: Pijoan-Mas 2006

[aledinola]

I’m testing the new grid interpolation feature of the toolkit in a model with a “d” variable (really happy about this addition to the toolkit ) and I found some bugs. The code is available in the online repo: GitHub - aledinola/PijoanMasTaxes: Aiyagari model with endogenous labor (as in Pijoan-Mas 2006), with VFI toolkit

These are my basic settings for VFI options:

vfoptions=struct(); 
vfoptions.lowmemory     = 0;
vfoptions.verbose       = 0;
vfoptions.tolerance     = 1e-6;
vfoptions.maxiter       = 500;
vfoptions.howards       = 80; 
vfoptions.maxhowards    = 500;
vfoptions.howardsgreedy = 0;

CASE 1
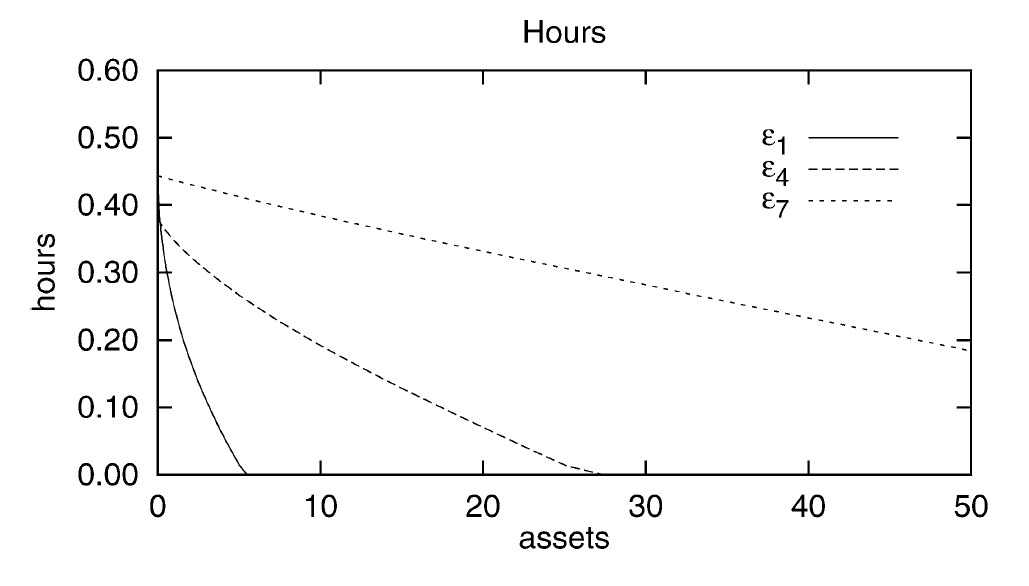
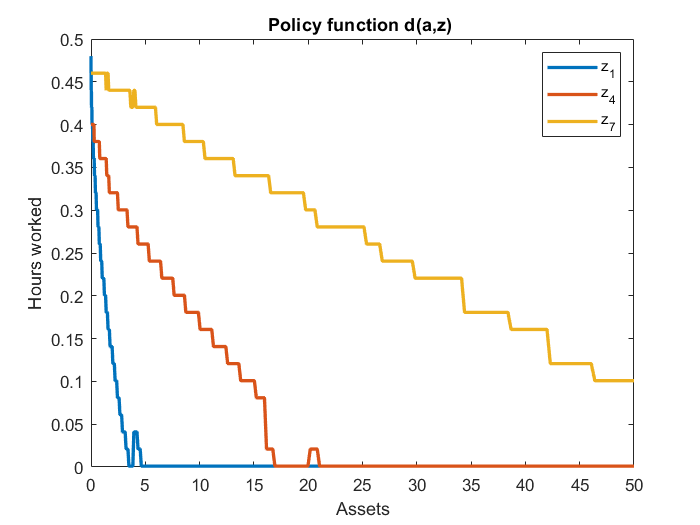
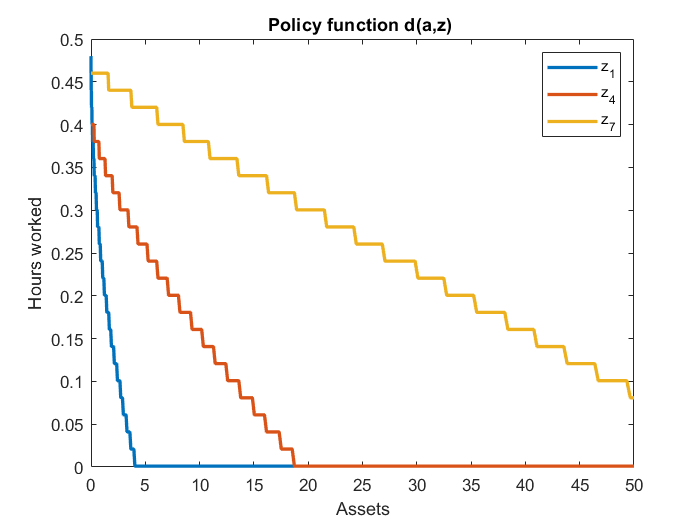
Without grid interpolation, all is good and I get these results (in partial equilibrium with HA maxiter=0):

Time VFI (seconds): 0.39
PARAMETERS
crra (Coeff of risk aversion)       : 1.458000 
nu (Curvature labor utility)        : 2.833000 
lambda (Weight of labor in disutil) : 0.856000 
beta (Discount factor)              : 0.945000 
theta (Labor share in Cobb-Douglas) : 0.640000 
delta (Capital depreciation rate)   : 0.083000 
lambda_hsv : 1.000000 
tau_hsv    : 0.000000 
------------------------------------
GENERAL EQUILIBRIUM PRICES
K_to_L : 5.534500 
r      : 0.037429 
w      : 1.184918 
------------------------------------
MOMENTS
Corr(h,z)  : NaN 
CV(h)      : 0.205128 
Hours      : 0.354671 
K/Y        : 3.013323 
w*L/Y      : 0.637126 
I/Y        : 0.250106 
------------------------------------
CV
CV(Hours)   : 0.205128 
CV(Earnings): 0.636984 
CV(Income)  : 0.624952 
CV(Wealth)  : 1.364293 
------------------------------------
GINI
Gini(Hours)   : 0.106121 
Gini(Earnings): 0.322589 
Gini(Income)  : 0.311692 
Gini(Wealth)  : 0.646641 
------------------------------------
CORR
corr(Hours,z) : NaN 
corr(Wealth,z): NaN 
------------------------------------
SHARES EARNINGS
q1 earnings: 0.074485 
q2 earnings: 0.124297 
q3 earnings: 0.173624 
q4 earnings: 0.229642 
q5 earnings: 0.397952 
------------------------------------
SHARES WEALTH
q1 wealth: 0.000706 
q2 wealth: 0.021652 
q3 wealth: 0.092324 
q4 wealth: 0.232139 
q5 wealth: 0.653179 

CASE 2
Now I set vfoptions.gridinterplayer=1; but I forget to set ngridinterp. I get this error:

Error using ValueFnIter_Case1 (line 71)
When using vfoptions.gridinterplayer=1 you must set vfoptions.gridinterplayer

The error message has a typo: it should read you must set vfoptions.ngridinterp

CASE 3
Now I remember to set both options:

vfoptions.gridinterplayer = 1;
vfoptions.ngridinterp     = 15;

but I get this new error message:

Error using gpuArray/reshape
Number of elements must not change. Use [] as one of the size inputs to automatically calculate the
appropriate size for that dimension.

Error in PolicyInd2Val_Case1 (line 202)
            Policy=reshape(Policy,[l_d+l_aprime,N_a*N_z]);
                   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in EvalFnOnAgentDist_AggVars_Case1 (line 156)
    PolicyValues=PolicyInd2Val_Case1(Policy,n_d,n_a,n_z,d_grid,a_grid,simoptions);
                 ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1_subfn (line 56)
AggVars=EvalFnOnAgentDist_AggVars_Case1(StationaryDist, Policy, FnsToEvaluateCell, Parameters, FnsToEvaluateParamNames, n_d, n_a, n_z, d_grid, a_grid, z_gridvals, simoptions);
        ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1>@(p)HeteroAgentStationaryEqm_Case1_subfn(p,n_d,n_a,n_z,d_grid,a_grid,z_grid,pi_z,ReturnFn,FnsToEvaluate,FnsToEvaluateCell,GeneralEqmEqnsCell,Parameters,DiscountFactorParamNames,ReturnFnParamNames,FnsToEvaluateParamNames,GeneralEqmEqnParamNames,GEPriceParamNames,GEeqnNames,AggVarNames,nGEprices,heteroagentoptions,simoptions,vfoptions) (line 609)
    GeneralEqmConditionsFnOpt=@(p) HeteroAgentStationaryEqm_Case1_subfn(p, n_d, n_a, n_z, d_grid, a_grid, z_grid, pi_z, ReturnFn, FnsToEvaluate, FnsToEvaluateCell, GeneralEqmEqnsCell, Parameters, DiscountFactorParamNames, ReturnFnParamNames, FnsToEvaluateParamNames, GeneralEqmEqnParamNames, GEPriceParamNames, GEeqnNames, AggVarNames, nGEprices, heteroagentoptions, simoptions, vfoptions);
                                   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1 (line 610)
    GeneralEqmConditions=GeneralEqmConditionsFnOpt(p_eqm_vec_untranformed);
                         ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

Low Memory
Note that the error reported above happens in the general equilibrium loop, not in the VFI per se. So I test now only the VFI but it is slow (see comment below). Maybe my 4 GB gpu works better with low memory, so I set

vfoptions.lowmemory     = 1;
vfoptions.verbose       = 0;
vfoptions.tolerance     = 1e-6;
vfoptions.maxiter       = 500;
vfoptions.howards       = 80; 
vfoptions.maxhowards    = 500;
vfoptions.howardsgreedy = 0;
vfoptions.gridinterplayer = 1;
vfoptions.ngridinterp     = 15;

but there is a new errro, this time in VFI, in function ValueFnIter_Refine_preGI_raw:

Unable to perform assignment because the size of the left side is 4785-by-300-by-1 and the size of the
right side is 300-by-1.

Error in ValueFnIter_Refine_preGI_raw (line 47)
        ReturnMatrixfine(:,:,z_c)=shiftdim(ReturnMatrixfine_z,1);
        ^^^^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_GridInterpLayer (line 58)
            [V,Policy]=ValueFnIter_Refine_preGI_raw(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
                       ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_Case1 (line 421)
    [V,Policy]=ValueFnIter_GridInterpLayer(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
               ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1_subfn (line 52)
[V,Policy]=ValueFnIter_Case1(n_d,n_a,n_z,d_grid,a_grid,z_gridvals, pi_z, ReturnFn, Parameters, DiscountFactorParamNames,ReturnFnParamNames,vfoptions);
           ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1>@(p)HeteroAgentStationaryEqm_Case1_subfn(p,n_d,n_a,n_z,d_grid,a_grid,z_grid,pi_z,ReturnFn,FnsToEvaluate,FnsToEvaluateCell,GeneralEqmEqnsCell,Parameters,DiscountFactorParamNames,ReturnFnParamNames,FnsToEvaluateParamNames,GeneralEqmEqnParamNames,GEPriceParamNames,GEeqnNames,AggVarNames,nGEprices,heteroagentoptions,simoptions,vfoptions) (line 609)
    GeneralEqmConditionsFnOpt=@(p) HeteroAgentStationaryEqm_Case1_subfn(p, n_d, n_a, n_z, d_grid, a_grid, z_grid, pi_z, ReturnFn, FnsToEvaluate, FnsToEvaluateCell, GeneralEqmEqnsCell, Parameters, DiscountFactorParamNames, ReturnFnParamNames, FnsToEvaluateParamNames, GeneralEqmEqnParamNames, GEPriceParamNames, GEeqnNames, AggVarNames, nGEprices, heteroagentoptions, simoptions, vfoptions);
                                   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1 (line 610)
    GeneralEqmConditions=GeneralEqmConditionsFnOpt(p_eqm_vec_untranformed);
                         ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

Other comments
The VFI runs surprisingly slow. My grid sizes are

Pijoan-Mas discretization of z with 7 points
n_a = 300, n_d = 51 

The bottleneck is in the function ValueFnIter_Refine_preGI_raw, line 27 when the code calls CreateReturnFnMatrix_Case2_Disc_Par2. On my laptop with 4 GB of RAM it takes 30 seconds. It could be that my gpu is not very good, but this is a small problem, so I am surprised.
Could it be that this algorithm is so memory-hungry (I thought the opposite was true but maybe I don’t have a clear understanding of the algo)? If I set anything bigger, it goes out of memory. Instead, without grid interpolation, I can set n_a=1000 and it works fine, albeit slow.

In the Pijoan-Mas model, one of the targeted moment is the correlation between hours of work d(a,z) and labor productivity z. Once the toolkit can compute correlations, I will add it to my example. For now, I left it NaN.

All in all, the toolkit is becoming more and more flexible over time

[robertdkirkby]

Fixed the typo in error message.

I think the error for general eqm was likely because you don’t set simoptions.gridinterplayer?, so have added an error message in general eqm command to warn if you set it in vfoptions but not simoptions.

I will look at the low memory and runtimes later.

[aledinola]

I added gridinterplayer to simoptions as follows:

vfoptions.gridinterplayer = 1;
vfoptions.ngridinterp     = 15;

% Distribution options
simoptions=struct(); % Use default options for solving for stationary distribution
simoptions.gridinterplayer = vfoptions.gridinterplayer;
simoptions.ngridinterp     = vfoptions.ngridinterp;

but now there is a new error message:

Unable to perform assignment because the size of the left side is 4785-by-300-by-1 and the size of
the right side is 300-by-1.

Error in ValueFnIter_Refine_preGI_raw (line 47)
        ReturnMatrixfine(:,:,z_c)=shiftdim(ReturnMatrixfine_z,1);
        ^^^^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_GridInterpLayer (line 58)
            [V,Policy]=ValueFnIter_Refine_preGI_raw(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
                       ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_Case1 (line 421)
    [V,Policy]=ValueFnIter_GridInterpLayer(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
               ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1_subfn (line 52)
[V,Policy]=ValueFnIter_Case1(n_d,n_a,n_z,d_grid,a_grid,z_gridvals, pi_z, ReturnFn, Parameters, DiscountFactorParamNames,ReturnFnParamNames,vfoptions);
           ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1>@(p)HeteroAgentStationaryEqm_Case1_subfn(p,n_d,n_a,n_z,d_grid,a_grid,z_grid,pi_z,ReturnFn,FnsToEvaluate,FnsToEvaluateCell,GeneralEqmEqnsCell,Parameters,DiscountFactorParamNames,ReturnFnParamNames,FnsToEvaluateParamNames,GeneralEqmEqnParamNames,GEPriceParamNames,GEeqnNames,AggVarNames,nGEprices,heteroagentoptions,simoptions,vfoptions) (line 614)
    GeneralEqmConditionsFnOpt=@(p) HeteroAgentStationaryEqm_Case1_subfn(p, n_d, n_a, n_z, d_grid, a_grid, z_grid, pi_z, ReturnFn, FnsToEvaluate, FnsToEvaluateCell, GeneralEqmEqnsCell, Parameters, DiscountFactorParamNames, ReturnFnParamNames, FnsToEvaluateParamNames, GeneralEqmEqnParamNames, GEPriceParamNames, GEeqnNames, AggVarNames, nGEprices, heteroagentoptions, simoptions, vfoptions);
                                   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1 (line 615)
    GeneralEqmConditions=GeneralEqmConditionsFnOpt(p_eqm_vec_untranformed);
                         ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

You can try out my code at GitHub - aledinola/PijoanMasTaxes: Aiyagari model with endogenous labor (as in Pijoan-Mas 2006), with VFI toolkit

By the way, I think also the Guerrieri and Lorenzoni example should generate the same error (infinite horizon model with a d variable)

[robertdkirkby]

Figured I’d better run an actual code should be fixed now [with and without lowmemory]

[aledinola]

Hi Rob,

Thanks! Now the VFI works but there is an error message in the stationary distribution.

Time VFI (seconds): 6.04 
Unrecognized function or variable 'StationaryDist_InfHorz_GI_raw'.

Error in StationaryDist_Case1 (line 273)
    StationaryDist=StationaryDist_InfHorz_GI_raw(StationaryDist,Policy,l_d,N_a,N_z,pi_z,simoptions);
    ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in solve_model_toolkit (line 78)
StationaryDist=StationaryDist_Case1(Policy,n_d,n_a,n_z,pi_z, simoptions);
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in main (line 104)
[Params,pol,mu,agg,mom] = solve_model_toolkit(par,grids,vfoptions,simoptions,heteroagentoptions);
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

You can see my code on github (see link in previous post).

By the way, the VFI with na=300, nd=51 and nz=7 runs in 0.4 seconds without interpolation and 6 seconds with interpolation (and 15 points in between). I think the slowdown is quite significant. Not sure if it depens on my GPU though. If you have time, could you please run my code with vfoptions.gridinterplayer = 0 and then 1 and let me know the run times? Thank you so much.

[robertdkirkby]

oops, was sitting on my harddrive but had missed it when pushing to github. Should be there now.

I had similar slowdown. I can see why (takes a few more iterations, and mostly because the max operation in each iteration takes much more time), less obvious is if there is something to be done about it (short of the kind of strong assumptions being used by MCA and the like).

[aledinola]

Thanks! Now it runs ok but the results are completely different from the case without interpolation

GeneralEqmCondn = 

  struct with fields:

    CapitalMarket: -131.537385062015

Without interpolation, the GE condition was

CapitalMarket: -0.0696377300801423

[robertdkirkby]

Probably fixed

(pushed a fix, haven’t had a chance to do much testing yet)

[aledinola]

Great, now it works!

Here is the plot of the policy function for hours worked, meant to replicate Fig 1 in Pijoan-Mas (2006). Hours worked is called d in the toolkit notation. Exogenous state for labor productuvuty, \varepsilon in the paper, is called z in the toolkit notation.

Original plot Pijoan-Mas (2006)

Policy d with grid interp = 0

Policy d with grid interp = 1

What is interesting to see is that interpolation is over a', not over d. Nonetheless, interpolation removes the strange kinks in the policy d(a,z).

Question

How do I plot the policy a'(a,z)? Now Policy has size [3,n_a,n_z]. My old plot for the case with grid interp=0 was like this:

pol_ind_ap = squeeze(Policy(2,:,:)); % a'(a,z)
pol_ap = a_grid(pol_ind_ap);

figure
plot(a_grid,a_grid,'--','LineWidth',2)
hold on
plot(a_grid,pol_ap(:,1),'LineWidth',2)
hold on
plot(a_grid,pol_ap(:,round(n_z/2)),'LineWidth',2)
hold on
plot(a_grid,pol_ap(:,n_z),'LineWidth',2)
xlabel('assets')
ylabel('aprime')
title('Policy function a''(a,z) ' )

But I guess the code above is now wrong, because it is plotting only the left-points for a'. How should I then plot a'(a,z)?

[robertdkirkby]

“What is interesting to see is that interpolation is over a′, not over d. Nonetheless, interpolation removes the strange kinks in the policy d(a,z).”
Makes sense, because the ‘interpolation’ is based on a finer grid on a’, and d is still solved exactly for this finer grid (the Return fn is exact, only the expected value fn is linearly interpolated). To say much the same in a different way, the ‘refine’ is done for the finer grid.

Easiest/recommended way to plot is just use PolicyInd2Vals commands to convert it to values, then plot those. If you want to DIY, then you can calculate the ‘fine grid index’ as (vfoptions.ngridinterp+1)*(Policy(2,:,:)-1)+Policy(3,:,:) and aprime_grid as interp1(linspace(1,N_a,N_a),a_grid,linspace(1,N_a,N_aprime)) where N_aprime=N_a+(N_a-1)*vfoptions.ngridinterp. Then you just do aprime_grid(fineindex) which is same step as your previous code did with pol_ap = a_grid(pol_ind_ap);

[aledinola]

@robertdkirkby

Makes sense, because the ‘interpolation’ is based on a finer grid on a’, and d is still solved exactly for this finer grid (the Return fn is exact, only the expected value fn is linearly interpolated). To say much the same in a different way, the ‘refine’ is done for the finer grid.

Maybe this is the reason why the code is slow. If I understood it correctly, the optimal d is precomputed for all possible (a',a,z) where a' is on the finer grid, so many grid points. I timed out different parts and the bottleneck is indeed the computation of the return matrix, not the vfi.

Is there a version of this code without refinement? Would it make sense at all to solve this model without refinement?

[robertdkirkby]

Would be even slower without refinement, because would still calculate the whole return matrix, but then just keep d in the problem while doing the iterations.

Because the toolkit does interpolation in the third way described in this post (skip to Ctrl-F “but allowing for interpolation of”) it comes with the advantage that the exact evaluation of the return fn means you don’t have to worry that, e.g., linear interpolation will cause the model to breach the constraints (implicit finite differences does breach them occasionally), and it will also be more accurate (for given original grid), but this comes with a runtime cost.

To cut the runtimes you would need something closer to the MCA (markov chain approximation) approach where you just assume that most values of a’ are ‘not allowed’ (in continuous time models this looks like the assumption that you can at most move up/down one grid point). That is, you need an assumption that slashes the choice-space.

In short, I suspect major speed gains would need to come from some strong assumptions that hold in some models but not others, like MCA. That said, if most of the runtime is the return fn it is good odds to fall a lot over the next few years with better gpus.

The good news is that with InfHorz models the toolkit is much better at transition paths than stationary general eqm, so can get some runtime back there

[aledinola]

I noticed that the option

vfoptions.howardsgreedy

takes on three values: 0,1 and 2

Can I choose Howards based on iterations with sparse matrix?
(I don’t want to use the algorithm based on \ because it is too memory intensive. The reason is that you have to build the sparse matrix T for the entire transitions from (a,z) to (a’,z’). This was the matrix we were using in the distribution iterations before discovering the Tan improvement and even though it is sparse it is still quite large

Thanks!

[robertdkirkby]

All of them do ‘multi-grid’, so they do VFI on the ‘original’ grid while currdist>multigridswitch*Tolerance, and then switch to VFI on ‘fine’ grid while currdist>Tolerance (currdist is the distance V-Vold; Tolerance default is 1e-9, multigridswich default is 10^4).

vfoptions.howardgreedy=0 uses Howards iteration, =1 uses Howard greedy, and then =2 is a mixture using Howards iteration on the ‘original’ grid and then Howards greedy on the ‘fine’ grid.

Because the run times for model without d variable were such that if there was any runtime difference between indexing and sparse matrix for implementing howards iterations, it was vanishingly small, I only did the indexing when doing models with d variable.

Note: if you want to disable multi-grid, just set vfoptions.multigridswitch=1/vfoptions.tolerance [codes use currdist=1 as the value before starting the VFI, specifically so that this works to disable multi-grid].

[aledinola]

Thanks for the answer! I will play around with these options, then.

I used the Pijoan-Mas model as a test; the real model I am currently working on has “action space” (d,a1',a2',a1,a2,z). Since it has two endogenous state variables, grid interpolation is not yet implemented (I am looking forward to this )

In any case, given the size of the problem (I have more than 70 nodes on z), I thought that Howard iteration with sparse matrix would be the best algorithm (where best means least memory intensive while retaining a decent speed). Indexing on the gpu is fast but uses more memory, right?

[robertdkirkby]

I don’t actually know if indexing uses more/less memory than sparse matrix multiplication. Not clear to me why indexing would. Both sparse and indexing need the location of the values, and with grid interpolation both also need the probabilities of the values.

That said, I didn’t run any test for sparse vs indexing in models with interpolation, only with pure discretization. So I guess maybe the answer could be different with interpolation than it was without.

[aledinola]

I tried running my Pijoan-Mas example with vfoptions.howardsgreedy = 2;

but I got this error:

Unrecognized function or variable 'Policy'.

Error in ValueFnIter_Refine_preGI_HowardMix_raw (line 96)
        tempmaxindex=shiftdim(Policy,1)+addindexforaz; % aprime index, add the index for a and z
                              ^^^^^^
Error in ValueFnIter_GridInterpLayer (line 62)
            [V,Policy]=ValueFnIter_Refine_preGI_HowardMix_raw(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
                       ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in ValueFnIter_Case1 (line 421)
    [V,Policy]=ValueFnIter_GridInterpLayer(V0, n_d, n_a, n_z, d_gridvals, a_grid, z_gridvals, pi_z, ReturnFn, DiscountFactorParamsVec, ReturnFnParamsVec, vfoptions);
               ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1_subfn (line 52)
[V,Policy]=ValueFnIter_Case1(n_d,n_a,n_z,d_grid,a_grid,z_gridvals, pi_z, ReturnFn, Parameters, DiscountFactorParamNames,ReturnFnParamNames,vfoptions);
           ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1>@(p)HeteroAgentStationaryEqm_Case1_subfn(p,n_d,n_a,n_z,d_grid,a_grid,z_grid,pi_z,ReturnFn,FnsToEvaluate,FnsToEvaluateCell,GeneralEqmEqnsCell,Parameters,DiscountFactorParamNames,ReturnFnParamNames,FnsToEvaluateParamNames,GeneralEqmEqnParamNames,GEPriceParamNames,GEeqnNames,AggVarNames,nGEprices,heteroagentoptions,simoptions,vfoptions) (line 614)
    GeneralEqmConditionsFnOpt=@(p) HeteroAgentStationaryEqm_Case1_subfn(p, n_d, n_a, n_z, d_grid, a_grid, z_grid, pi_z, ReturnFn, FnsToEvaluate, FnsToEvaluateCell, GeneralEqmEqnsCell, Parameters, DiscountFactorParamNames, ReturnFnParamNames, FnsToEvaluateParamNames, GeneralEqmEqnParamNames, GEPriceParamNames, GEeqnNames, AggVarNames, nGEprices, heteroagentoptions, simoptions, vfoptions);
                                   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in HeteroAgentStationaryEqm_Case1 (line 615)
    GeneralEqmConditions=GeneralEqmConditionsFnOpt(p_eqm_vec_untranformed);
                         ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in solve_model_toolkit (line 54)
[p_eqm,~,GeneralEqmCondn]=HeteroAgentStationaryEqm_Case1(n_d, n_a, n_z, 0, pi_z, d_grid, a_grid, z_grid, ReturnFn, FnsToEvaluate, GeneralEqmEqns, Params, DiscountFactorParamNames, [], [], [], GEPriceParamNames,heteroagentoptions, simoptions, vfoptions);
                          ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Error in main (line 104)
[Params,Policy,StatDist,agg,mom] = solve_model_toolkit(par,grids,vfoptions,simoptions,heteroagentoptions);
                                   ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

[robertdkirkby]

Fixed. (I copy pasted some code across, forgot to rename a variable)

[aledinola]

Thanks for fixing this. There is still an error with interp=0 and howardsgreedy=2 (please see below). I ran some tests in partial equilibrium (i.e. with GE maxiter=0) and the run times for VFI are the following:

Grid sizes
n_d=101, n_a=301, n_z=7, ngridinterp=15 (relevant only if gridinterp=1)

gridinterp	howardsgreedy	VFI Run time in secs
0	0	0.72
0	1	1.04
0	2	Error
1	0	11.25
1	1	11.56
1	2	11.30

A couple of considerations from this table:

1. There is no meaningful difference between the three howards greedy options, at least for grid interp =1. Without interpolation, howardsgreedy=0 seems slightly faster than howardsgreedy=1. howardsgreedy=2 without interpolation gives an error.
2. There is quite a significant slowdown moving from no interpolation to interpolation. The code with interpolation is about 11/0.7= 15 times slower In general equilibrium it would take a long time to solve these models. I am a bit surprised since the fhorz with interpolation shows a decent performance.

P.S. My comparison is not entirely fair to the code with interpolation. To keep a similar degree of accuracy, I would set n_a without interpolation to something like n_a=600 or 700, so the pure discretization run time would become a bit worse

[robertdkirkby]

Yeah, the interpolation in finite horizon seems to be a 10-30% slowdown, which is pretty minor cost for the increased accuracy. An important part of the difference is that in FHorz I can do ‘two layers’ so I only interpolate either side of one grid point (the optimal one from the first layer), while in the InfHorz I need to precompute and so I interpolate everywhere (I did a runtime test, and once I precompute the fine return fn there was no point using layers anymore).

My approach is always first to get things working, and then later I can come back and look at how to speed up. If you look at the number of iterations it is massively higher for the interpolation version, which suggests this is the bottleneck and a good target for runtime improvements. (You would have to uncomment the counter which is a line of code in the VFI codes; run code, press Ctrl+C halfway through, and the error msg links you directly to the relevant subcode . It is not normally reported to the user because unless you are looking to modify internal code it doesn’t seem likely to be useful info.)

The error is just because there is no such thing as vfoptions.gridinterplayer=0 and vfoptions.howardsgreedy=2. You can only set vfoptions.howardsgreedy=2 when using vfoptions.gridinterplayer=1.

One option for general eqm is that I go and add that you can do a multi-grid approach, so it would first roughly solve the GE using gridinterplayer=0 and then do GE with gridinterplayer=1 to clean it up. I will likely do this, maybe next week (is already mostly done, as is used for doing a rough-but-fast optimization algo, then switching to a slower optimization algo to clean up). In models with more GE condns this will probably help.